Open: Обработка конформационных ансамблей в Python: Difference between revisions
m (→Quick start) |
|||
| (190 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
===Этот мануал не сделан для того, чтобы читать его до конца. Остановитесь ровно тогда, когда поймете, как решать стоящую перед вами задачу.=== | |||
==В чем заключается эта обработка и для чего её делать?== | ==В чем заключается эта обработка и для чего её делать?== | ||
| Line 16: | Line 15: | ||
* Объединить конформационные ансамбли из нескольких расчетов, полученные, например, как в пункте выше, и отсортировать структуры по их энергии. | * Объединить конформационные ансамбли из нескольких расчетов, полученные, например, как в пункте выше, и отсортировать структуры по их энергии. | ||
Этот мануал посвящен моей библиотеке [https:// | Этот мануал посвящен моей библиотеке [https://gitlab.com/knvvv/pyxyz pyxyz], которая позволяет решать эти задачи несколькими строчками в Python. Также этот мануал может быть полезен при анализе XYZ-файлов, полученных в результате расчета молекулярной динамики, оптимизаций, сканов, IRC и т.п. | ||
== | ==Релевантные Wiki-статьи== | ||
[[Конформационный поиск|Мануал Вадима Малышева о том, как делать расчеты]], где есть раздел про конформационный поиск - задача, в которой быстрое фильтрование по RMSD однозначно пригодится. | |||
[[Нахождение дубликатов структур|Статья о библиотеке chemistryR Артёма Дмитриенко]] - более медленная, но проверенная многими людьми имплементация фильтрования по RMSD на языке R. Фильтрование по RMSD, реализованное в pyxyz, действует по том же алгоритму, что и в chemistryR. | |||
[[Установка и настройка Jupyter Notebook на сервере|Статья о запуске Jupyter Notebook]] - полезная среда для интерактивной работы с кодом на Python и, в особенности, с кодом, использущим pyxyz. | |||
<big>'''Все инструкции этого мануала продублированы в [https://knvvv.gitlab.io/pyxyz/ документации PyXYZ]'''</big> | |||
==Установка библиотеки== | |||
Для работы под Linux требуется Python версии 3.8 или выше. Windows на данный момент не поддерживается (если хотите об этом поговорить - пишите [https://t.me/Nkrivoshchapov сюда]). Установка необходимых библиотек Python: | |||
<source lang="bash"> | |||
pip install numpy networkx plotnine jupyter plotly | |||
# If the above doesn't work, try | |||
pip3 install numpy networkx plotnine jupyter plotly | |||
</source> | |||
Для установки нужно выполнить в терминале следующую команду: | |||
<source lang="bash"> | |||
pip install --upgrade pyxyz24 | |||
# If the above doesn't work, try | |||
pip3 install --upgrade pyxyz24 | |||
</source> | |||
Обратите внимание, что в некоторых случаях может понадобиться заменить pip на pip3 (это зависит от того, как у вас установлен Python). | Обратите внимание, что в некоторых случаях может понадобиться заменить pip на pip3 (это зависит от того, как у вас установлен Python). | ||
| Line 34: | Line 48: | ||
После вызова pip install проверьте корректность установки: импортируется ли библиотека и выполняются ли тесты: | После вызова pip install проверьте корректность установки: импортируется ли библиотека и выполняются ли тесты: | ||
<source lang="python"> | |||
import pyxyz | |||
import pyxyz.test | |||
pyxyz.test.run_tests() | |||
</source> | |||
== | Если вам зачем-то ооочень надо запустить pyxyz под Windows, то можете попробовать старую версию: | ||
<source lang="bash"> | |||
pip install -i https://test.pypi.org/simple/ "pyxyz>=1.0" | |||
</source> | |||
==Quick start== | |||
Все необходимые действия написаны в Jupyter Notebook'e. Весь этот раздел - это комментарии к тому, что в нем делается: | |||
<big>'''[https://gitlab.com/knvvv/pyxyz/-/blob/master/example_notebook/demo.ipynb?ref_type=heads Notebook для удаления дубликатов]'''</big> | |||
Скачать можно так: | |||
wget https://gitlab.com/knvvv/pyxyz/-/raw/master/example_notebook/demo.ipynb | |||
wget https://gitlab.com/knvvv/pyxyz/-/raw/master/example_notebook/initial_set.xyz | |||
Зайдите через терминал в папку с файлом ''demo.ipynb'', выполните | |||
jupyter notebook demo.ipynb | |||
Затем, следуйте указаниям в заголовках и комментариях в коде. | |||
Задача удаления дубликатов, которую решает код в ''demo.ipynb'', очень часто возникает при анализе конформационных наборов. Чтобы опознать, что две структуры являются дубликатами, нам нужна метрика "похожести" структур молекул. В качестве этой метрики обычно используют [https://en.wikipedia.org/wiki/Root-mean-square_deviation_of_atomic_positions RMSD]: чем меньше RMSD пары конформеров, тем их геометрии более близки. | |||
[[File:RMSD meaning.png|center|thumb|upright=2.0|Геометрический смысл RMSD (говоря полностью - RMSD декартовых координат атомов для пары наложенных друг на друга конформаций).]] | |||
В библиотеке pyxyz реализован достаточно быстрый алгоритм расчета RMSD, однако остается несколько вопросов: | |||
# Какое выбрать пороговое значение RMSD, ниже которого пары структур считаются одинаковыми? | |||
# Как определить топологию (связи) молекулы, которая необходима для выявления эквивалентных атомов? | |||
# Как ускорить фильтрование по RMSD для очень больших наборов конформеров с минимальными потерями в надежности? | |||
На все три вопроса есть решения, но они требуют от пользователя понимания происходящего. Необходимая информация по каждому из вопросов приведена ниже: | |||
===Выбор порогового RMSD=== | |||
Вопрос критичный, так как, если выбранное пороговое значение слишком низкое, то много дубликатов останутся неотфильтроваными, а если слишком высокое, то некоторые уникальные конформеры будут ошибочно удалены. Принцип поиска порогового RMSD прост: (1) смотрим на распределение значений RMSD для всех пар структур конформационного ансамбля, видим маленький пик пар дубликатов вблизи нуля и большой пик пар отличающихся структур, начинающийся около 1 А, (2) выбираем значение RMSD, в котором маленький пик пропал, а большой ещё не начался, (3) смотрим на пары вблизи этого RMSD и убеждаемся, что при таком выборе порога мы не потеряем уникальных конформеров. | |||
[[File:RMSD cutoff figure.png|center|thumb|upright=2.0|Принцип выбора порогового значение RMSD для фильтрования дубликатов. Код для построения таких картинок есть в архиве "Notebook для удаления дубликатов"]] | |||
===Определение связей в молекуле=== | |||
Этот вопрос тоже критичный, так как, если связи в молекуле расставлены неправильно, то могут быть упущены (или найдены лишние) эквивалентные атомы, что приведет к заниженным/завышенным RMSD. Определение связей из положений атомов делается автоматически на основании ковалентных радиусов. Однако, нужно проконтролировать, что связи были действительно сгенерированы верно, особенно, когда некоторые связи почему-то удлинены (т.е. явно выше суммы ковалентных радиусов, например, в случае конфпоиска переходных состояний). Функция ''generate_connectivity'' имеет флаг ''sdf_name'' для сохранения топологии в отдельный файл, который можно открыть и проверить корректность расстановки связей. | |||
===Фильтрование идет слишком долго. Как ускорить?=== | |||
* '''Исключение атомов водорода.''' Это уменьшит количество эквивалентных атомов и ускорит расчет RMSD. Для этого в вызове ''generate_connectivity'' замените ''ignore_elements=[]'' на ''ignore_elements=['HCarbon']''. | |||
* '''Сравнивать энергии вместо RMSD.''' Ключ ''energy_threshold'' в вызове ''rmsd_filter'' задает минимальную разницу в энергях конформеров, при которой можно не считать RMSD и говорить, что эти конформеры отличаются. В коде выше эта величина выбрана за 1.0 ккал/моль, но можно её немного уменьшить для большей скорости фильтрования. | |||
* '''Исключение высокоэнергетических конформеров.''' Это уменьшит количество рассматриваемых конформеров и, соответственно, количество расчетов RMSD, которое нужно делать. Для этого в вызове ''upper_cutoff'' надо уменьшить пороговую энергию с 10.0 ккал/моль на что-то поменьше в зависимости от того, насколько вы доверяете методу расчета энергии. | |||
* '''Запустите тоже самое под Linux.''' Опыт показывает, что на нём работает быстрее. | |||
* '''Исключение малоинтересующих структур на основании их геометрии.''' Например, если ваша молекула может образовывать внутримолекулярную водородную связь, то почему бы не отбросить все структуры ею не обладающие (после расчета DFT они всё равно окажутся высокоэнергетическими)? Про то, как делать это и многое другое, написано в следующем разделе. | |||
==Как написать свой скрипт для обработки конформационных наборов?== | |||
<big>'''Архив с примерами -- [https://theorchem.ru/mediawiki/images/d/dc/Pyxyz_manual.zip Pyxyz_manual.zip]'''</big> ([[File:Pyxyz manual.zip|thumb]]) | <big>'''Архив с примерами -- [https://theorchem.ru/mediawiki/images/d/dc/Pyxyz_manual.zip Pyxyz_manual.zip]'''</big> ([[File:Pyxyz manual.zip|thumb]]) | ||
В качестве примера рассмотрим | В качестве примера рассмотрим конформационные наборы переходного состояния из файлов crest_conformersA.xyz и crest_conformersB.xyz (см. архив). Рассмотрим несколько учебных задач, которые могли бы возникнуть на практике. Обратите внимание, что в пределах одного объекта Confpool количество атомов в анализируемых молекулах и последовательность атомов в импортируемых xyz-файлах должны быть одинаковыми. | ||
= | Для работы потребуются следующие импорты: | ||
<source lang="python"> | |||
from pyxyz import Confpool, KC2H, H2KC # Coefficients of kcal <-> Hartree conversions | |||
import numpy as np | |||
</source> | |||
Для большей интерактивности с библиотекой можно работать не только запуская код из файла, но и через jupyter notebook. | |||
[[File:TS for pyxyz.png|thumb|upright=1.8|Рисунок 1. Геометрия ПС, для которого сделан конфпоиск]] | |||
===Базовая обработка конформационных наборов=== | |||
=== | Допустим, мы сделали два запуска CREST и получили два файла с конформациями crest_conformersA.xyz и crest_conformersB.xyz. Для начала, загружаем оба xyz-файла в один объект Confpool: | ||
<source lang="python"> | |||
p = Confpool() | |||
p.include_from_file("crest_conformersA.xyz") | |||
p.include_from_file("crest_conformersB.xyz") | |||
print(f"Loaded {p.size} conformers") | |||
</source> | |||
Для дальнейшей обработки кроме геометрий нам понадобятся энергии конформеров. Их можно извлечь из описания к структурам: | |||
<source lang="python"> | |||
n_del = 0 | |||
p["Energy"] = lambda m: float(m.descr.strip()) | |||
n_del += p.upper_cutoff("Energy", 5.0 * KC2H) | |||
print(f"{n_del} confs were filtered out") | |||
p.sort("Energy") # Ascending by default. Use ascending=False to override | |||
</source> | |||
Четвертая строчка здесь самая интересная - в ней мы говорим, что каждой конформации нужно сопоставить ключ ''Energy'' и рассчитать его из описания к конформации с помощью [https://www.geeksforgeeks.org/passing-function-as-an-argument-in-python/ переданной функции] (strip удаляет ненужные пробелы, а float конвертирует в дробное число). Далее мы применям '''upper_cutoff''', чтобы отбросить все конформеры с энергией выше 5 ккал/моль относительно минимальной энергии в наборе, и сортируем по возрастанию энергии. Стоит отметить, что все операции, сопровождающиеся удалением конформеров из набора (всего их четыре: '''filter''', '''rmsd_filter''', '''upper_cutoff''', '''lower_cutoff'''), возвращают целое число - количество удаленных структур, либо словарь, в котором это число записано под ключом ''DelCount''. Завершаем обработку отбрасыванием дубликатов по RMSD (приведенный ниже код работает очень медленно в случае данного ПС, см. ниже, как его легко ускорить): | |||
<source lang="python"> | |||
p.generate_connectivity(0, mult=1.3, add_bonds=[[13, 23]], sdf_name='connectivity_check.sdf') | |||
p.generate_isomorphisms() | |||
n_del += p.rmsd_filter(0.3, print_status=True)['DelCount'] | |||
print(f"{n_del} confs were filtered in total") | |||
p.descr = lambda m: "Conf #{}; Energy = {:6f} a.u.".format(m.idx + 1, m["Energy"]) | |||
p.save_xyz('basic_processing.xyz') | |||
</source> | |||
Перед тем как фильтровать дубликаты по RMSD надо сделать два подготовительных этапа: сгенерировать топологию, а затем - изоморфизмы. Функция ''generate_connectivity'' определяет топологию (связи) в молекуле, используя ковалентные радиусы. То есть, если расстояние между парой атомов меньше, чем сумма их ковалентных радиусов, умноженная на ''mult'', то эти два атома считаются связанными. Выбор связей можно проконтролировать вручную с помощью кейвордов ''add_bonds'' и ''remove_bonds''. Нуль первым аргументом означает, что связи генерируется на основании первой структуры в наборе. Можно попросить программу записать сгенерированную топологию в sdf-файл, если передать в функцию ''generate_connectivity'' ключ ''sdf_name'' (требуемое название файла). Такая возможность позволяет подобрать подходящее значение ''mult'' и убедиться, что топология выбрана правильно. После успешной генерации топологии, надо сгенерировать изоморфизмы вызовом функции ''generate_isomorphisms''. | |||
Для собственно поиска дубликатов мы передали критерий для фильтрования RMSD < 0.3 A. Затем для оставшихся уникальных конформеров обновили описание с помощью переданной lambda-функции и сохранили набор в файл. Чтобы получить более хорошее представление о том, какой RMSD cutoff стоит брать, вместе с вызовом ''rmsd_filter'' можно сделать следующее: | |||
<source lang="python"> | |||
p.rmsd_filter(0.3, print_status=True) # Very slow due to huge number of symmetries | |||
min_rmsd, min_pair = pyxyz.smallest_rmsd_pair(p.get_rmsd_matrix()) | |||
newp = Confpool() | |||
newp.include_subset(p, min_pair) | |||
newp.save_xyz("rmsd_test.xyz") | |||
print(f"The smallest accepted RMSD is {min_rmsd}") | |||
</source> | |||
Здесь создается ещё один набор с парой структур, соответствующих минимальному RMSD > rmsd_cutoff. Посмотрев, насколько сильно отличаются геометрии в файле rmsd_test.xyz можно попытаться оптимизировать rmsd_cutoff. Если почти не отличаются, то надо увеличивать. Слишком разные - уменьшать. | |||
Для очень больших конформационных наборов или очень симметричных молекул может возникнуть проблема скорости работы '''rmsd_filter'''. Для этого можно выбросить атомы каких-то элементов, обычно Н, а ещё можно использовать разницу значений какого-то ключа, как повод не считать RMSD для данной пары (все варианты ускорения уже были приведены в предыдущем разделе). Выполнив приведенный ниже код, можете убедиться, что удаление связанных с углеродом атомов водорода уменьшает количество изоморфизмов с 10368 до 8. | |||
<source lang="python"> | |||
# For faster filtration use this | |||
p.generate_connectivity(0, mult=1.3, add_bonds=[[13, 23]], ignore_elements=['HCarbon']) | |||
niso_a = p.generate_isomorphisms() | |||
p.rmsd_filter(0.3, energy_threshold=1.0 * KC2H, energy_key='Energy', print_status=True) | |||
# instead of this | |||
p.generate_connectivity(0, mult=1.3, add_bonds=[[13, 23]]) | |||
niso_b = p.generate_isomorphisms() | |||
print(f"{niso_b} vs. {niso_a} improvement when ignoring HCarbon atoms") | |||
print("The next maneuver is gonna cost us 51 years...") | |||
p.rmsd_filter(0.3, print_status=True) | |||
</source> | |||
В листе ''ignore_elements'' можно передавать символы обычных элементов, типа 'H' или 'F', тогда все атомы этих элементов будут исключены из расчетов изоморфизмов и расчетов RMSD. Также специально имплементирован ещё один тип игнорируемых атомов 'HCarbon', включение которого в ''ignore_elements'' приведет к игнорированию не всех атомов 'H', а только тех, которые образуют связь с одними атомом 'C' и больше ни с чем. | |||
Получив финальный конформационный набор, можно не только сохранить его в xyz, а ещё и сгенерировать input-файлы для оптимизации или какого-то другого вида расчета: | |||
<source lang="python"> | |||
gjftemplate = """\ | |||
%nprocs=24 | |||
# opt=(tight,maxcycle=300) freq=noraman def2tzvp empiricaldispersion=gd3bj rpbe1pbe scrf=(cpcm,solvent=water) | |||
Conformation_{idx} | |||
0 1 | |||
{xyz} | |||
""" | |||
atom_symbols = p.atom_symbols | |||
for i, m in enumerate(p): | |||
xyz = m.xyz # xyz is a Numpy matrix | |||
xyzlines = [] | |||
for j, symbol in enumerate(atom_symbols): | |||
xyzlines.append("%2s %14.6f %14.6f %14.6f" % (symbol, *xyz[j])) | |||
with open(f"conf_{i}.gjf", 'w') as f: | |||
f.write(gjftemplate.format(xyz="\n".join(xyzlines), idx=i)) | |||
</source> | |||
В 90% случаев, как мне кажется, на этом этапе потребности расчетчика должны уже быть удовлетворены. Но иногда может захотеться обработать структуры более детально. | |||
== | ===Анализ геометрии=== | ||
Продолжаем работу над объектом p, полученным в предыдущей секции. Как видно из Рисунка 1, явная молекула воды была добавлена, чтобы стабилизировать атом водорода 26, но в ходе конфпоиска H2O могла перескочить на другие атомы. Чтобы понять, сколько структур содержат интересующую нас водородную связь H26-O27, можно выполнить следующий код: | |||
<source lang="python"> | |||
p["H2O dist"] = lambda m: m.l(26, 27) | |||
for m in p: | |||
print("Length = {}".format(m["H2O dist"])) | |||
# Could also use | |||
for i in range(p.size): | |||
print("Length = {}".format(p[i].l(26, 27))) | |||
# or | |||
print("Length = {}".format(p[i]["H2O dist"])) | |||
# Analyze the printed numbers and then | |||
print("Found {} good structures".format(p.count(lambda m: m["H2O dist"] < 1.8))) | |||
</source> | |||
Мы здесь использовали функцию '''m.l(a, b)''', чтобы обратиться к длинам связи отдельной структуры в наборе (внутри lambda-функции и при обращении по индексу). И ещё пригодилась функция '''count''', чтобы посчитать количество структур, удовлетворяющих заданному условию. Небольшое отступление: удобством в обращении по ключу в цикле, т.е. '''m["H2O dist"]''' или '''p[i]["H2O dist"]''', является возможность поменять значение ключа только для определенной структуры, например, '''p[i]["H2O dist"] = 123.0'''; но в текущей задаче это не понадобилось. | |||
=== | Далее можно отобразить наличие нужно водородной связи в описании структуры: | ||
<source lang="python"> | |||
def quality_check(m): | |||
if m["H2O dist"] < 1.8: | |||
comment = "Nice" | |||
else: | |||
comment = "Garbage" | |||
return "{}; E={:3f} a.u.".format(comment, m["Energy"]) | |||
# Print new descriptions in the console | |||
for m in p: | |||
print(quality_check(m)) | |||
= | p.descr = quality_check # Set new descriptions | ||
p.save_xyz('hbond_analysis.xyz') | |||
</source> | |||
Если нужно наложить какие-то сложные требования на геометрию, то это можно сделать в одну строчку. Валентные и торсионные углы вычисляются функциями '''m.v(a, b, c)''' и '''m.z(a, b, c, d)''', соответственно: | |||
<source lang="python"> | |||
hbond_condition = lambda m: m.l(25, 10) < 2.0 and m.v(24, 25, 10) > 150.0 and abs(m.z(26, 23, 24, 25)) > 120.0 | |||
print("There are {} matches".format(p.count(hbond_condition))) | |||
p.filter(hbond_condition) | |||
min_ener = min(p["Energy"]) # p["Energy"] creates a list of floats | |||
p["E.Rel"] = lambda m: H2KC * (m["Energy"] - min_ener) | |||
p.descr = lambda m: "{}; E(rel.)={:3f} kcal/mol".format(m.descr, m["E.Rel"]) | |||
p.save_xyz('extreme_hbond_analysis.xyz') | |||
</source> | |||
''' | Не считая сложного условия '''hbond_condition''', в части с фильтрованием всё очевидно. А вот во второй части кода есть особенности: обращением '''p["Energy"]''' можно получать лист значений некого существующего ключа, а при установке новых значений '''p.descr''' или '''p["Some key"]''' можно обращаться к их старым значениям. | ||
===Тонкости работы с библиотекой=== | |||
Как вы уже могли заметить, библиотека сделана исходя из нескольких ограничений: | |||
# Все структуры подаются с одинаковой нумерацией атомов. Если дать две структуры с нумерациями C1, H2, H3 и H1, C2, H3, то будет Exception. | |||
# Кроме XYZ, каждой структуре сопоставляется одна строка '''m.descr''' и сколько угодно дробных чисел '''m["SomeKey"]''', к которым можно обращаться по ключу (ключами могут быть только строки). Попытка записать по ключу что-то кроме дробного числа приведет к исключению (аналогично, с нестрочными описаниями структур). | |||
# Все структуры имеют одинаковый набор ключей. | |||
Вернемся к задаче с переходным состоянием с Рисунка 1 и допустим, что мы хотим проанализировать, насколько энергетически выгодны конформации, заданные критерием '''hbond_condition(m) and m.l(26, 27) < 1.8''', на фоне остальных найденных конформаций. | |||
<source lang="python"> | |||
import pandas as pd | |||
p = Confpool() | |||
p.include_from_file("crest_conformersA.xyz") | |||
p.include_from_file("crest_conformersB.xyz") | |||
p["Energy"] = lambda m: float(m.descr.strip()) | |||
p.sort("Energy") | |||
p.generate_connectivity(0) | |||
p.generate_isomorphisms() | |||
p.rmsd_filter(0.3) | |||
for m in p: | |||
if hbond_condition(m) and m.l(26, 27) < 1.8: | |||
m["MyCondition"] = 1.0 # Just 1 would give an error | |||
else: | |||
m["MyCondition"] = 0.0 # Same here with 0 | |||
print(pd.DataFrame(p.as_table())) | |||
</source> | |||
В результате мы получили DataFrame, в котором MyCondition соответствует тому, выполняются наши требования на водородные связи или нет: | |||
MyCondition Energy | |||
0 0.0 -45.344433 | |||
1 0.0 -45.343703 | |||
2 1.0 -45.343607 | |||
3 0.0 -45.343443 | |||
4 0.0 -45.342388 | |||
5 1.0 -45.342137 | |||
... | |||
Здесь, мы пользуемся небольшим костылём в связи с тем, что ключи обязаны быть дробными числами, поэтому ''"MyCondition"'' - дробное число, а не bool, например. Чтобы об этом не забывать, никакие неявные конверсии во время присвоения не делаются (см. выше, что '''с дробным числом''' 1.0 '''работает''', а '''с целым числом''' 1 - '''нет'''). Другой момент - это что присвоение значения нового ключа для одной структуры автоматически инициализирует этот ключ со значением 0.0 для всех остальных структур (см. третий принцип в начале раздела). Ну и, наконец, '''p.as_table()''' генерирует вам данные всех ключей в виде словаря из листов. | |||
Ещё полезно знать о возможности создания копий объектов Confpool. | |||
<source lang="python"> | |||
# All these calls won't modify the original pool (p) | |||
p_new = Confpool(p) # Creates a copy of p | |||
p_new = p.sort("Energy", inplace=False) # Returns a modified copy of p | |||
res = p.upper_cutoff("Energy", 2.0 * KC2H, inplace=False) | |||
p_new = res['Object'] | |||
print(f"New pool ({p_new.size}) has {res['DelCount']} less structures compared to the initial one ({p.size})") | |||
''' | res = p.lower_cutoff("Energy", 2.0 * KC2H, inplace=False) | ||
p_new = res['Object'] # Returns a modified copy of p | |||
print(f"New pool ({p_new.size}) has {res['DelCount']} less structures compared to the initial one ({p.size})") | |||
res = p.filter(lambda m: '69' in str(m["Energy"]), inplace=False) | |||
p_new = res['Object'] # Returns a modified copy of p | |||
print(f"The nice pool ({p_new.size}) has {res['DelCount']} less structures compared to the initial one ({p.size})") | |||
res = p.rmsd_filter(0.2, inplace=False) | |||
p_new = res['Object'] # Returns a modified copy of p | |||
print(f"New pool ({p_new.size}) has {res['DelCount']} less structures compared to the initial one ({p.size})") | |||
</source> | |||
Небольшой комментарий насчет возможных багов: изоморфизмы без проблем копируются из старого объекта в новый, однако с молекулярным графом могут быть проблемы, так что, во избежание багов, перед вызовом '''generate_isomorphisms''' для нового объекта делайте для него вызов '''generate_connectivity'''. | |||
<source lang="python"> | |||
# Case 1 - OK. p_new inherits isomorphisms from p | |||
p_new = Confpool(p) | |||
p_new.rmsd_filter(0.2) # OK if generate_connectivity and generate_isomorphisms were called for p | |||
= | # Case 2 - might be bugged. Inherit molecular graph but generate isomorphisms from scratch | ||
p_new = Confpool(p) | |||
p_new.generate_isomorphisms() | |||
p_new.rmsd_filter(0.2) | |||
1. | # Case 3 - OK. Generate graph AND isomorphisms from scratch | ||
p_new = Confpool(p) | |||
p_new.generate_connectivity(0, mult=1.3) | |||
p_new.generate_isomorphisms() | |||
p_new.rmsd_filter(0.2) | |||
</source> | |||
Ещё добавлю, что можно достаточно легко удалять ненужные структуры и ключи: | |||
<source lang="python"> | |||
del p[0] | |||
del p[p.size - 1] | |||
del p["MyKey"] | |||
</source> | |||
Этот код удаляет первую и последнюю структуры в наборе, а затем удаляет ключ ''"MyKey"'' для всех оставшихся структур. | |||
Для особо заинтересовавшихся на [https://knvvv.gitlab.io/pyxyz/source/pyxyz.html сайте с документацией] приведен весь функционал библиотеки с короткими примерами кода. | |||
TODO | ==TODO== | ||
# Вариация класса Confpool для произвольных структур без ограничений на типы атомов | |||
# Вариации класса Confpool с ключами произвольного (mutable) типа и значениями типа py::object. | |||
# Search for VdW contacts | |||
# copy constructor, operator+ | |||
# Прикрутить библиотеку, которая парсит логи квантовохимических программ | |||
Latest revision as of 21:25, 9 October 2025
Этот мануал не сделан для того, чтобы читать его до конца. Остановитесь ровно тогда, когда поймете, как решать стоящую перед вами задачу.
В чем заключается эта обработка и для чего её делать?
Программы для конформационного поиска обычно выдают результаты в виде XYZ файлов, структуры из которых обычно надо вписать в инпут-файлы для последующей квантовохимической оптимизации. Чтобы уменьшить количество расчетов вам может захотеться сделать следующие операции, перед тем, как генерировать инпут-файлы:
- Отсеять конформации с чрезмерно высокой энергией;
- Удалить дубликаты;
- Проверить сохранение констрейнов и отбросить структуры, в которых они нарушены. Например, когда вы ищите конформеры переходного состояния в CREST, полученный конформационный набор может содержать структуры, в которых заданные констрейны сильно нарушены. Если начнете оптимизировать такие геометрии в DFT, то ПС не найдется, а вы потратите время.
- Проанализировать ансамбль и узнать, какие слабые взаимодействия (водородные связи и т.п.) могут образовываться в вашей молекуле. Найденные контакты можно учесть в дополнительных запусках конформационного поиска с констрейнами, чтобы лучше перебрать варианты с данными взаимодействиями.
- Объединить конформационные ансамбли из нескольких расчетов, полученные, например, как в пункте выше, и отсортировать структуры по их энергии.
Этот мануал посвящен моей библиотеке pyxyz, которая позволяет решать эти задачи несколькими строчками в Python. Также этот мануал может быть полезен при анализе XYZ-файлов, полученных в результате расчета молекулярной динамики, оптимизаций, сканов, IRC и т.п.
Релевантные Wiki-статьи
Мануал Вадима Малышева о том, как делать расчеты, где есть раздел про конформационный поиск - задача, в которой быстрое фильтрование по RMSD однозначно пригодится.
Статья о библиотеке chemistryR Артёма Дмитриенко - более медленная, но проверенная многими людьми имплементация фильтрования по RMSD на языке R. Фильтрование по RMSD, реализованное в pyxyz, действует по том же алгоритму, что и в chemistryR.
Статья о запуске Jupyter Notebook - полезная среда для интерактивной работы с кодом на Python и, в особенности, с кодом, использущим pyxyz.
Все инструкции этого мануала продублированы в документации PyXYZ
Установка библиотеки
Для работы под Linux требуется Python версии 3.8 или выше. Windows на данный момент не поддерживается (если хотите об этом поговорить - пишите сюда). Установка необходимых библиотек Python:
pip install numpy networkx plotnine jupyter plotly
# If the above doesn't work, try
pip3 install numpy networkx plotnine jupyter plotly
Для установки нужно выполнить в терминале следующую команду:
pip install --upgrade pyxyz24
# If the above doesn't work, try
pip3 install --upgrade pyxyz24
Обратите внимание, что в некоторых случаях может понадобиться заменить pip на pip3 (это зависит от того, как у вас установлен Python).
После вызова pip install проверьте корректность установки: импортируется ли библиотека и выполняются ли тесты:
import pyxyz
import pyxyz.test
pyxyz.test.run_tests()
Если вам зачем-то ооочень надо запустить pyxyz под Windows, то можете попробовать старую версию:
pip install -i https://test.pypi.org/simple/ "pyxyz>=1.0"
Quick start
Все необходимые действия написаны в Jupyter Notebook'e. Весь этот раздел - это комментарии к тому, что в нем делается:
Notebook для удаления дубликатов
Скачать можно так:
wget https://gitlab.com/knvvv/pyxyz/-/raw/master/example_notebook/demo.ipynb wget https://gitlab.com/knvvv/pyxyz/-/raw/master/example_notebook/initial_set.xyz
Зайдите через терминал в папку с файлом demo.ipynb, выполните
jupyter notebook demo.ipynb
Затем, следуйте указаниям в заголовках и комментариях в коде.
Задача удаления дубликатов, которую решает код в demo.ipynb, очень часто возникает при анализе конформационных наборов. Чтобы опознать, что две структуры являются дубликатами, нам нужна метрика "похожести" структур молекул. В качестве этой метрики обычно используют RMSD: чем меньше RMSD пары конформеров, тем их геометрии более близки.
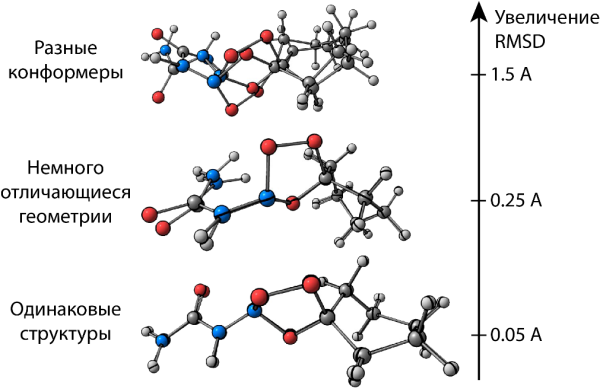
В библиотеке pyxyz реализован достаточно быстрый алгоритм расчета RMSD, однако остается несколько вопросов:
- Какое выбрать пороговое значение RMSD, ниже которого пары структур считаются одинаковыми?
- Как определить топологию (связи) молекулы, которая необходима для выявления эквивалентных атомов?
- Как ускорить фильтрование по RMSD для очень больших наборов конформеров с минимальными потерями в надежности?
На все три вопроса есть решения, но они требуют от пользователя понимания происходящего. Необходимая информация по каждому из вопросов приведена ниже:
Выбор порогового RMSD
Вопрос критичный, так как, если выбранное пороговое значение слишком низкое, то много дубликатов останутся неотфильтроваными, а если слишком высокое, то некоторые уникальные конформеры будут ошибочно удалены. Принцип поиска порогового RMSD прост: (1) смотрим на распределение значений RMSD для всех пар структур конформационного ансамбля, видим маленький пик пар дубликатов вблизи нуля и большой пик пар отличающихся структур, начинающийся около 1 А, (2) выбираем значение RMSD, в котором маленький пик пропал, а большой ещё не начался, (3) смотрим на пары вблизи этого RMSD и убеждаемся, что при таком выборе порога мы не потеряем уникальных конформеров.
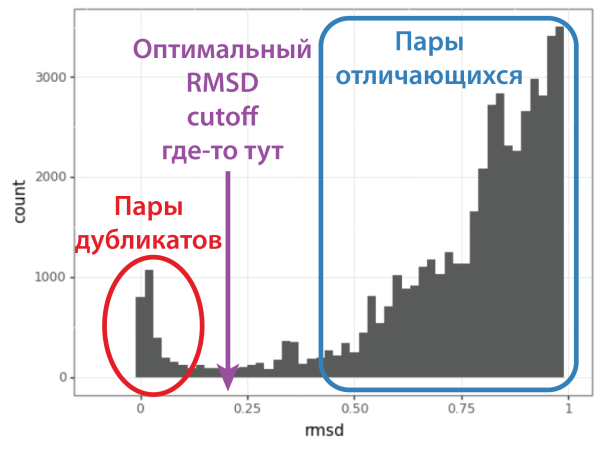
Определение связей в молекуле
Этот вопрос тоже критичный, так как, если связи в молекуле расставлены неправильно, то могут быть упущены (или найдены лишние) эквивалентные атомы, что приведет к заниженным/завышенным RMSD. Определение связей из положений атомов делается автоматически на основании ковалентных радиусов. Однако, нужно проконтролировать, что связи были действительно сгенерированы верно, особенно, когда некоторые связи почему-то удлинены (т.е. явно выше суммы ковалентных радиусов, например, в случае конфпоиска переходных состояний). Функция generate_connectivity имеет флаг sdf_name для сохранения топологии в отдельный файл, который можно открыть и проверить корректность расстановки связей.
Фильтрование идет слишком долго. Как ускорить?
- Исключение атомов водорода. Это уменьшит количество эквивалентных атомов и ускорит расчет RMSD. Для этого в вызове generate_connectivity замените ignore_elements=[] на ignore_elements=['HCarbon'].
- Сравнивать энергии вместо RMSD. Ключ energy_threshold в вызове rmsd_filter задает минимальную разницу в энергях конформеров, при которой можно не считать RMSD и говорить, что эти конформеры отличаются. В коде выше эта величина выбрана за 1.0 ккал/моль, но можно её немного уменьшить для большей скорости фильтрования.
- Исключение высокоэнергетических конформеров. Это уменьшит количество рассматриваемых конформеров и, соответственно, количество расчетов RMSD, которое нужно делать. Для этого в вызове upper_cutoff надо уменьшить пороговую энергию с 10.0 ккал/моль на что-то поменьше в зависимости от того, насколько вы доверяете методу расчета энергии.
- Запустите тоже самое под Linux. Опыт показывает, что на нём работает быстрее.
- Исключение малоинтересующих структур на основании их геометрии. Например, если ваша молекула может образовывать внутримолекулярную водородную связь, то почему бы не отбросить все структуры ею не обладающие (после расчета DFT они всё равно окажутся высокоэнергетическими)? Про то, как делать это и многое другое, написано в следующем разделе.
Как написать свой скрипт для обработки конформационных наборов?
Архив с примерами -- Pyxyz_manual.zip (File:Pyxyz manual.zip)
В качестве примера рассмотрим конформационные наборы переходного состояния из файлов crest_conformersA.xyz и crest_conformersB.xyz (см. архив). Рассмотрим несколько учебных задач, которые могли бы возникнуть на практике. Обратите внимание, что в пределах одного объекта Confpool количество атомов в анализируемых молекулах и последовательность атомов в импортируемых xyz-файлах должны быть одинаковыми.
Для работы потребуются следующие импорты:
from pyxyz import Confpool, KC2H, H2KC # Coefficients of kcal <-> Hartree conversions
import numpy as np
Для большей интерактивности с библиотекой можно работать не только запуская код из файла, но и через jupyter notebook.
Базовая обработка конформационных наборов
Допустим, мы сделали два запуска CREST и получили два файла с конформациями crest_conformersA.xyz и crest_conformersB.xyz. Для начала, загружаем оба xyz-файла в один объект Confpool:
p = Confpool()
p.include_from_file("crest_conformersA.xyz")
p.include_from_file("crest_conformersB.xyz")
print(f"Loaded {p.size} conformers")
Для дальнейшей обработки кроме геометрий нам понадобятся энергии конформеров. Их можно извлечь из описания к структурам:
n_del = 0
p["Energy"] = lambda m: float(m.descr.strip())
n_del += p.upper_cutoff("Energy", 5.0 * KC2H)
print(f"{n_del} confs were filtered out")
p.sort("Energy") # Ascending by default. Use ascending=False to override
Четвертая строчка здесь самая интересная - в ней мы говорим, что каждой конформации нужно сопоставить ключ Energy и рассчитать его из описания к конформации с помощью переданной функции (strip удаляет ненужные пробелы, а float конвертирует в дробное число). Далее мы применям upper_cutoff, чтобы отбросить все конформеры с энергией выше 5 ккал/моль относительно минимальной энергии в наборе, и сортируем по возрастанию энергии. Стоит отметить, что все операции, сопровождающиеся удалением конформеров из набора (всего их четыре: filter, rmsd_filter, upper_cutoff, lower_cutoff), возвращают целое число - количество удаленных структур, либо словарь, в котором это число записано под ключом DelCount. Завершаем обработку отбрасыванием дубликатов по RMSD (приведенный ниже код работает очень медленно в случае данного ПС, см. ниже, как его легко ускорить):
p.generate_connectivity(0, mult=1.3, add_bonds=[[13, 23]], sdf_name='connectivity_check.sdf')
p.generate_isomorphisms()
n_del += p.rmsd_filter(0.3, print_status=True)['DelCount']
print(f"{n_del} confs were filtered in total")
p.descr = lambda m: "Conf #{}; Energy = {:6f} a.u.".format(m.idx + 1, m["Energy"])
p.save_xyz('basic_processing.xyz')
Перед тем как фильтровать дубликаты по RMSD надо сделать два подготовительных этапа: сгенерировать топологию, а затем - изоморфизмы. Функция generate_connectivity определяет топологию (связи) в молекуле, используя ковалентные радиусы. То есть, если расстояние между парой атомов меньше, чем сумма их ковалентных радиусов, умноженная на mult, то эти два атома считаются связанными. Выбор связей можно проконтролировать вручную с помощью кейвордов add_bonds и remove_bonds. Нуль первым аргументом означает, что связи генерируется на основании первой структуры в наборе. Можно попросить программу записать сгенерированную топологию в sdf-файл, если передать в функцию generate_connectivity ключ sdf_name (требуемое название файла). Такая возможность позволяет подобрать подходящее значение mult и убедиться, что топология выбрана правильно. После успешной генерации топологии, надо сгенерировать изоморфизмы вызовом функции generate_isomorphisms.
Для собственно поиска дубликатов мы передали критерий для фильтрования RMSD < 0.3 A. Затем для оставшихся уникальных конформеров обновили описание с помощью переданной lambda-функции и сохранили набор в файл. Чтобы получить более хорошее представление о том, какой RMSD cutoff стоит брать, вместе с вызовом rmsd_filter можно сделать следующее:
p.rmsd_filter(0.3, print_status=True) # Very slow due to huge number of symmetries
min_rmsd, min_pair = pyxyz.smallest_rmsd_pair(p.get_rmsd_matrix())
newp = Confpool()
newp.include_subset(p, min_pair)
newp.save_xyz("rmsd_test.xyz")
print(f"The smallest accepted RMSD is {min_rmsd}")
Здесь создается ещё один набор с парой структур, соответствующих минимальному RMSD > rmsd_cutoff. Посмотрев, насколько сильно отличаются геометрии в файле rmsd_test.xyz можно попытаться оптимизировать rmsd_cutoff. Если почти не отличаются, то надо увеличивать. Слишком разные - уменьшать.
Для очень больших конформационных наборов или очень симметричных молекул может возникнуть проблема скорости работы rmsd_filter. Для этого можно выбросить атомы каких-то элементов, обычно Н, а ещё можно использовать разницу значений какого-то ключа, как повод не считать RMSD для данной пары (все варианты ускорения уже были приведены в предыдущем разделе). Выполнив приведенный ниже код, можете убедиться, что удаление связанных с углеродом атомов водорода уменьшает количество изоморфизмов с 10368 до 8.
# For faster filtration use this
p.generate_connectivity(0, mult=1.3, add_bonds=[[13, 23]], ignore_elements=['HCarbon'])
niso_a = p.generate_isomorphisms()
p.rmsd_filter(0.3, energy_threshold=1.0 * KC2H, energy_key='Energy', print_status=True)
# instead of this
p.generate_connectivity(0, mult=1.3, add_bonds=[[13, 23]])
niso_b = p.generate_isomorphisms()
print(f"{niso_b} vs. {niso_a} improvement when ignoring HCarbon atoms")
print("The next maneuver is gonna cost us 51 years...")
p.rmsd_filter(0.3, print_status=True)
В листе ignore_elements можно передавать символы обычных элементов, типа 'H' или 'F', тогда все атомы этих элементов будут исключены из расчетов изоморфизмов и расчетов RMSD. Также специально имплементирован ещё один тип игнорируемых атомов 'HCarbon', включение которого в ignore_elements приведет к игнорированию не всех атомов 'H', а только тех, которые образуют связь с одними атомом 'C' и больше ни с чем.
Получив финальный конформационный набор, можно не только сохранить его в xyz, а ещё и сгенерировать input-файлы для оптимизации или какого-то другого вида расчета:
gjftemplate = """\
%nprocs=24
# opt=(tight,maxcycle=300) freq=noraman def2tzvp empiricaldispersion=gd3bj rpbe1pbe scrf=(cpcm,solvent=water)
Conformation_{idx}
0 1
{xyz}
"""
atom_symbols = p.atom_symbols
for i, m in enumerate(p):
xyz = m.xyz # xyz is a Numpy matrix
xyzlines = []
for j, symbol in enumerate(atom_symbols):
xyzlines.append("%2s %14.6f %14.6f %14.6f" % (symbol, *xyz[j]))
with open(f"conf_{i}.gjf", 'w') as f:
f.write(gjftemplate.format(xyz="\n".join(xyzlines), idx=i))
В 90% случаев, как мне кажется, на этом этапе потребности расчетчика должны уже быть удовлетворены. Но иногда может захотеться обработать структуры более детально.
Анализ геометрии
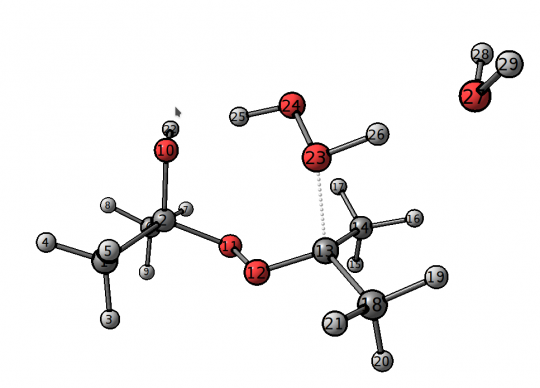
Продолжаем работу над объектом p, полученным в предыдущей секции. Как видно из Рисунка 1, явная молекула воды была добавлена, чтобы стабилизировать атом водорода 26, но в ходе конфпоиска H2O могла перескочить на другие атомы. Чтобы понять, сколько структур содержат интересующую нас водородную связь H26-O27, можно выполнить следующий код:
p["H2O dist"] = lambda m: m.l(26, 27)
for m in p:
print("Length = {}".format(m["H2O dist"]))
# Could also use
for i in range(p.size):
print("Length = {}".format(p[i].l(26, 27)))
# or
print("Length = {}".format(p[i]["H2O dist"]))
# Analyze the printed numbers and then
print("Found {} good structures".format(p.count(lambda m: m["H2O dist"] < 1.8)))
Мы здесь использовали функцию m.l(a, b), чтобы обратиться к длинам связи отдельной структуры в наборе (внутри lambda-функции и при обращении по индексу). И ещё пригодилась функция count, чтобы посчитать количество структур, удовлетворяющих заданному условию. Небольшое отступление: удобством в обращении по ключу в цикле, т.е. m["H2O dist"] или p[i]["H2O dist"], является возможность поменять значение ключа только для определенной структуры, например, p[i]["H2O dist"] = 123.0; но в текущей задаче это не понадобилось.
Далее можно отобразить наличие нужно водородной связи в описании структуры:
def quality_check(m):
if m["H2O dist"] < 1.8:
comment = "Nice"
else:
comment = "Garbage"
return "{}; E={:3f} a.u.".format(comment, m["Energy"])
# Print new descriptions in the console
for m in p:
print(quality_check(m))
p.descr = quality_check # Set new descriptions
p.save_xyz('hbond_analysis.xyz')
Если нужно наложить какие-то сложные требования на геометрию, то это можно сделать в одну строчку. Валентные и торсионные углы вычисляются функциями m.v(a, b, c) и m.z(a, b, c, d), соответственно:
hbond_condition = lambda m: m.l(25, 10) < 2.0 and m.v(24, 25, 10) > 150.0 and abs(m.z(26, 23, 24, 25)) > 120.0
print("There are {} matches".format(p.count(hbond_condition)))
p.filter(hbond_condition)
min_ener = min(p["Energy"]) # p["Energy"] creates a list of floats
p["E.Rel"] = lambda m: H2KC * (m["Energy"] - min_ener)
p.descr = lambda m: "{}; E(rel.)={:3f} kcal/mol".format(m.descr, m["E.Rel"])
p.save_xyz('extreme_hbond_analysis.xyz')
Не считая сложного условия hbond_condition, в части с фильтрованием всё очевидно. А вот во второй части кода есть особенности: обращением p["Energy"] можно получать лист значений некого существующего ключа, а при установке новых значений p.descr или p["Some key"] можно обращаться к их старым значениям.
Тонкости работы с библиотекой
Как вы уже могли заметить, библиотека сделана исходя из нескольких ограничений:
- Все структуры подаются с одинаковой нумерацией атомов. Если дать две структуры с нумерациями C1, H2, H3 и H1, C2, H3, то будет Exception.
- Кроме XYZ, каждой структуре сопоставляется одна строка m.descr и сколько угодно дробных чисел m["SomeKey"], к которым можно обращаться по ключу (ключами могут быть только строки). Попытка записать по ключу что-то кроме дробного числа приведет к исключению (аналогично, с нестрочными описаниями структур).
- Все структуры имеют одинаковый набор ключей.
Вернемся к задаче с переходным состоянием с Рисунка 1 и допустим, что мы хотим проанализировать, насколько энергетически выгодны конформации, заданные критерием hbond_condition(m) and m.l(26, 27) < 1.8, на фоне остальных найденных конформаций.
import pandas as pd
p = Confpool()
p.include_from_file("crest_conformersA.xyz")
p.include_from_file("crest_conformersB.xyz")
p["Energy"] = lambda m: float(m.descr.strip())
p.sort("Energy")
p.generate_connectivity(0)
p.generate_isomorphisms()
p.rmsd_filter(0.3)
for m in p:
if hbond_condition(m) and m.l(26, 27) < 1.8:
m["MyCondition"] = 1.0 # Just 1 would give an error
else:
m["MyCondition"] = 0.0 # Same here with 0
print(pd.DataFrame(p.as_table()))
В результате мы получили DataFrame, в котором MyCondition соответствует тому, выполняются наши требования на водородные связи или нет:
MyCondition Energy 0 0.0 -45.344433 1 0.0 -45.343703 2 1.0 -45.343607 3 0.0 -45.343443 4 0.0 -45.342388 5 1.0 -45.342137 ...
Здесь, мы пользуемся небольшим костылём в связи с тем, что ключи обязаны быть дробными числами, поэтому "MyCondition" - дробное число, а не bool, например. Чтобы об этом не забывать, никакие неявные конверсии во время присвоения не делаются (см. выше, что с дробным числом 1.0 работает, а с целым числом 1 - нет). Другой момент - это что присвоение значения нового ключа для одной структуры автоматически инициализирует этот ключ со значением 0.0 для всех остальных структур (см. третий принцип в начале раздела). Ну и, наконец, p.as_table() генерирует вам данные всех ключей в виде словаря из листов.
Ещё полезно знать о возможности создания копий объектов Confpool.
# All these calls won't modify the original pool (p)
p_new = Confpool(p) # Creates a copy of p
p_new = p.sort("Energy", inplace=False) # Returns a modified copy of p
res = p.upper_cutoff("Energy", 2.0 * KC2H, inplace=False)
p_new = res['Object']
print(f"New pool ({p_new.size}) has {res['DelCount']} less structures compared to the initial one ({p.size})")
res = p.lower_cutoff("Energy", 2.0 * KC2H, inplace=False)
p_new = res['Object'] # Returns a modified copy of p
print(f"New pool ({p_new.size}) has {res['DelCount']} less structures compared to the initial one ({p.size})")
res = p.filter(lambda m: '69' in str(m["Energy"]), inplace=False)
p_new = res['Object'] # Returns a modified copy of p
print(f"The nice pool ({p_new.size}) has {res['DelCount']} less structures compared to the initial one ({p.size})")
res = p.rmsd_filter(0.2, inplace=False)
p_new = res['Object'] # Returns a modified copy of p
print(f"New pool ({p_new.size}) has {res['DelCount']} less structures compared to the initial one ({p.size})")
Небольшой комментарий насчет возможных багов: изоморфизмы без проблем копируются из старого объекта в новый, однако с молекулярным графом могут быть проблемы, так что, во избежание багов, перед вызовом generate_isomorphisms для нового объекта делайте для него вызов generate_connectivity.
# Case 1 - OK. p_new inherits isomorphisms from p
p_new = Confpool(p)
p_new.rmsd_filter(0.2) # OK if generate_connectivity and generate_isomorphisms were called for p
# Case 2 - might be bugged. Inherit molecular graph but generate isomorphisms from scratch
p_new = Confpool(p)
p_new.generate_isomorphisms()
p_new.rmsd_filter(0.2)
# Case 3 - OK. Generate graph AND isomorphisms from scratch
p_new = Confpool(p)
p_new.generate_connectivity(0, mult=1.3)
p_new.generate_isomorphisms()
p_new.rmsd_filter(0.2)
Ещё добавлю, что можно достаточно легко удалять ненужные структуры и ключи:
del p[0]
del p[p.size - 1]
del p["MyKey"]
Этот код удаляет первую и последнюю структуры в наборе, а затем удаляет ключ "MyKey" для всех оставшихся структур.
Для особо заинтересовавшихся на сайте с документацией приведен весь функционал библиотеки с короткими примерами кода.
TODO
- Вариация класса Confpool для произвольных структур без ограничений на типы атомов
- Вариации класса Confpool с ключами произвольного (mutable) типа и значениями типа py::object.
- Search for VdW contacts
- copy constructor, operator+
- Прикрутить библиотеку, которая парсит логи квантовохимических программ